Датировка по пасхе
Датировка по пасхе. Как отмечал выдающийся специалист по хронологии профессор Петербургской духовной академии В. В. Болотов (1854—1900), знание пасхалии особенно важно в отношении к средним векам, «когда господствовала своеобразная манера обозначения дат. Светский человек чувствует себя здесь, как в лесу. Вместо того чтобы обозначать время по числам и дням месяца, обозначали по дням памяти святых... Самое распространенное обыкновение было, напр., обозначать воскресенье словами праздничного гимна».
И там, где датировка воскресных дней производилась словами праздничных гимнов, весь календарь в буквальном смысле этого слова был связан с пасхой. Скорее даже с «пятидесятницей» («троицей»), так как отсюда церковь ведет счет дней (недель) в году: «1-я неделя по пятидесятнице», «2-я неделя...» и т. д. вплоть до «недели мытаря и фарисея», которой, однако, как бы начинается новый пасхальный цикл. В Западной Европе с пасхой даже связали на несколько столетий самое начало нового года.
Вот примеры датирования документов по пасхе и связанным с нею «подвижным праздникам».
Радонежским князем Андреем Владимировичем была выдана жалованная грамота игумену Троице-Сергиева монастыря Никону, дата же определена так: «А дана грамота коли князь великий княжну отдал во Царь на ту зиму на вербницу» («вербница», «вербная неделя» — вторая неделя перед пасхой). Летопись указывает, что великий князь Василий Дмитриевич отдал дочь за греческого царевича Ивана в 1411 г., пасха в этом году приходилась на 12 апреля, вербное же воскресенье на 5 апреля. Следовательно, грамота была дана «на вербной неделе» — в промежутке между 30 марта и 5 апреля.
А вот сообщение о том, что великий художник «Рафаэль умер в ночь на святую пятницу 1520 г.». Пасха в 1520 г. приходилась на 8 апреля, «великая», или «святая» пятница — на 6 апреля. Следовательно, Рафаэль умер в ночь с 5 на 6 апреля 1520 г.
Прибавим еще текст дарственной надписи, сделанной В. А. Жуковским на портрете, подаренном А. С. Пушкину: «Победителю-ученику от побежденного учителя в тот высокоторжественный день, в который он окончил свою поэму «Руслан и Людмила». 1820, марта 26, великая пятница». Использовав приведенные далее таблицы и формулы, читатель установит, что дата здесь указана правильно, так как пасха в 1820 г. действительно была 28 марта.
«Ключи границ». По установленным в IV в. правилам христианская пасха должна праздноваться в первое воскресенье после первого весеннего полнолуния. Но вместо точных расчетов астрономических фаз Луны на каждый год используется «расписание фаз Луны» по месяцам 19-летнего метонова цикла, датой же весеннего равноденствия было принято считать 21 марта. Итог такой «связки» двух календарей — солнечного и лунного, каждый из которых обладал своими внутренними недостатками, известен— вынужденная реформа 1582 г., и об этом еще речь впереди. Здесь мы ограничимся кратким изложением главных принципов, лежащих в основе расчетов дат пасхи.
1. Если полнолуние наступит 21 марта и этот день — суббота, то датой пасхи будет 22 марта. Это ее самый ранний срок. Когда же полнолуние придется на 19 марта («расписание фаз Луны» таково, что 20 марта оно не бывает), то весенним считается следующее (19 + 30 — 31 = ) 18 апреля. И в случае, когда этот день — воскресенье, пасха переносится на следующее воскресенье — на 25 апреля. Это ее наиболее поздний срок. Таким образом, пасха может выпасть на один из 35 дней — от 22 марта по 25 апреля.
2. Дни от 22 марта по 25 апреля обозначаются 35 буквами славянского алфавита от «аза» до «юса малого», называются они ключевыми или пасхальными буквами, это также — ключи границ (от латинского granes — «край листа», так как в описании пасхалии их печатали крупным шрифтом на краях страниц). Ключам границ можно придать также числовые значения z, обозначив их от z = 1 («аз») до z = 35 («юс малый») . Тем самым дата пасхи определяется как (21+z) марта или при z > 10 (z—10) апреля ст. ст. Тем самым упрощается и расчет других связанных с пасхой дат.
Например, дата уже упомянутой недели «мытаря и фарисея» определяется как 10 января + z (в високосном году—11 января+ z), «троица» — 9 мая + z и т. д. Знание числа z позволяло устанавливать и контролировать дни недели, приходящиеся на отдельные церковные праздники, а тем самым и на другие календарные числа. Например, день недели, на которую пришлось в каком-то году с известным z «благовещение» (25 марта) определяется как
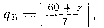а день «Георгия победоносца» (23 апреля) как
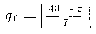и т. д. Числовой порядок дней в неделе здесь таков: понедельник—1, вторник — 2 и т. д.
3. Уже в V в. н. э. было составлено расписание новолуний на 19-летний лунный цикл, которое и используется неизменно до сих пор для определения пасхальных фаз Луны. На этой основе уже было нетрудно рассчитать и даты весенних полнолуний для каждого круга Луны. Дата пасхи устанавливалась элементарно в два приема:
а) Сначала определялось место, которое занимает данный год в 19-летнем лунном цикле, т. е. его круг Луны L и тем самым по табл. — дата весеннего полнолуния для этого года.
б) рассчитывался круг Солнца Q и находилось вруцелето W данного года, в результате чего и устанавливалось, на какой день недели пришлось это полнолуние. После этого находилась дата ближайшего за ним воскресенья — пасхи.
Сказанное дало возможность сопоставить даты пасхи (и соответствующие им ключи границ) с кругами Луны и вруцелетами, как это показано в табл.
Таблица. Соответствие дат пасхи ключевым буквам, вруцелетам и кругам Луны (м — март, а — апрель)
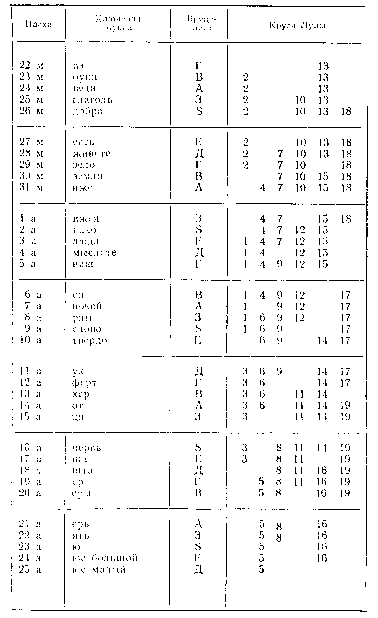
Из нее находим, что при упомянутом в Псковской летописи ключе границ Р пасха приходится на 8 апреля, чему соответствует вруцелето 3 и круг Луны 17. Как видим, все эти элементы датировки в данном примере полностью согласуются друг с другом, Из табл. находим, что как круг Луны L, так и круг Солнца Q соответствуют году «от Адама» 6496.
Теперь можно установить и смысл данных в табл. исправных букв. Это ключи границ, приходящиеся на числа месяцев, которые в данном году следуют сразу же после полнолуния (на следующий день!). Они указывают дату «ущерба» (фазу Луны «полнолуние плюс один день») и дают в соответствии с табл. наиболее раннюю дату, на которую (если «ущерб» приходится на воскресенье) в данном году может выпасть пасха. Определение исправной буквы года — одна из основных задач календарных расчетов, которые проводились на Руси на протяжении многих веков. Излишне подчеркивать, что ее расчет имел и самостоятельное значение, ведь ею определяется дата весеннего полнолуния!
Отметим, что через 19 X 28 = 532 года фазы Луны (расчетные!) и дни недели приходятся на те же числа месяца. Поэтому через каждые 532 года полностью повторяются и даты пасхи. Этот промежуток времени был назван великим индиктионом. Индиктионы было принято отсчитывать от начала византийской эры. В частности, 12-й великий индиктион начался в 345 г., 13-й —в 877 г., 14-й —в 1409 г., 15-й великий индиктион начался в 1941 г.
Формулы Гаусса. Возможности сопоставления и проверки многих документов и летописных датировок значительно возросли после того как выдающийся немецкий математик Карл Фридрих Гаусс (1777—1855) вывел формулы для непосредственного определения дат христианской и еврейской пасхи. В частности, по формулам для еврейской пасхи с высокой точностью устанавливается дата истинного (астрономического) весеннего полнолуния, что позволяет проверить — могло быть или кет в указанное летописцем время, скажем, солнечное или лунное затмение и др. Об этих формулах речь пойдет далее.
Схема расчета даты католической пасхи выглядит так. Разделив сначала число года R на 19, 4 и 7, получаем соответственно остатки a, b и с. Далее находим величину 19ах, делим ее на 30 и остаток обозначаем d. После этого составляем сумму 2b + 4с + 6d + у и делим ее на 7, остаток обозначаем через е. Пасха будет 22 + (d + e) марта н. ст. или,
если d + e больше 10, (d + e) — 9 апреля н. ст. Величины х и у равны соответственно
с 1582 по 1699 гг. 22 и 2,
с 1700 по 1799 гг. 23 и 3,
с 1800 по 1899 гг. 23 и 4,
с 1900 по 2099 гг. 24 и 5.
Пределы здесь те же, что и в православной пасхалии — с 22 марта по 25 апреля (однако — нового стиля!). При этом формулы предусматривают два исключения: 1) если (d+e) — 9 = 26 апреля, то пасха переносится на 19 апреля (это относится к годам 1609, 1981, 2076 и 2133), и 2) если d = 28 и е = 6, так что (d+e) — 9 = 25, то пасха переносится на 18 апреля (такое случилось в 1954 г. и будет в 2049 и 2106 гг.).
Расчет даты православной пасхи проводится по той же схеме, но при постоянных значениях величин x и у. х = 15 и у = 6. Результат получается в датах по ст. ст.
Отметим, что остаток d определяет число дней, на которое в R-м году пасхальное полнолуние отошло от своего предела — 21 марта, величина (е+1) — число дней от пасхального полнолуния до первого после него воскресенья. Остаток от деления величины 5b + Зс + 4 на 7 определяет вруцелето года.
Рассчитаем теперь дату пасхи на 1411 г., когда «на вербницу» была дана упомянутая выше жалованная грамота. Разделив 1411 на 19, 4 и 7, находим остатки а = 5, b= 3 и с = 4. Составляем величину 19а + 15 = 110 и делим ее на 30, в остатке получаем d = 20. Далее находим величину 26 + 4с + 6d + 6 = 2Х 3 + 4 X 4 + 6 X 20 + 6 = 148 и, разделив ее на 7, находим в остатке е— 1. Следовательно, пасха в 1411 г. приходилась на (d + e) — 9 = (20+1) — 9 = 12 апреля ст. ст.
Вывод и объяснение отдельных этапов формул Гаусса даны в статье Г. Кинкелина.